こんにちは。

いつもクラ・ゼミ札幌東苗穂校第２のブログをご覧下さり、誠に有難うございます。

壁紙は令和５年９月バージョンです。

今回も職員とお子様方が協力して作ってくれました。

お月様と月見団子のコラボレーションが秀逸です。👏👏👏

今回は年長さんや小学生のお子様方に関するお話です。

あなたのお子様は、数をきちんと数えたり、その量をマッチングすることが出来ますか？

また、足し算や引き算などの計算をスムーズに出来ますか？

支援している中で、どうしても計算が苦手なお子様が多いです。

指を使わないと計算が苦手であったり、繰り上がりの計算になると答えが出せなかったり。

また、文章を見た時に足し算か引き算なのかが分からなかったり…。

あなたのお子様はいかがでしょうか？

実は、計算をしっかりと出来るようにするには、

数の２つの概念の習得が必須なのです。

今回は、数に関しての大切な２つの概念のご紹介と、その概念の育て方をお伝えします。

これが分かれば、お家でも上手に数について教えることが出来ますよ！

〇数の三項関係の確立が大前提！

ちょっと小難しいお話になることをお許し下さい。

２つのチカラというのがタイトルですが、

まずは、数の三項関係というものが確立

しているのが前提となります。

これは、数字と数詞と具体物が一致していることを指します。

例えばですが、数字は「３」で数詞は「さん」ということ、

具体物であれば「イチゴが３個」などですね。

まずはこれらが一致していることが、数の概念を習得する大前提となります。

数字のことがまだ全然理解出来ていなかったら、無理をせずにこの部分を固めて下さい。

では、次に数の２つの概念についてお話します。

〇序数性(じょすうせい)

これは、「序」と書いているだけあって、

数の順序に関する概念です。

先ほどの数の三項関係がある程度育っていれば、

その流れに沿って順番などを覚えていけると思います。

そのため、ある時に突然育っているなんていうこともあり得ます。

この序数性が弱いと、「５の次は何？」と聞くと止まったり、

初めから数え直したりします。

要は、頭の中に数直線のようなものが確立されていないんですね。

数えることがこの概念の形成に大きく繋がりますので、

目の前の物を一緒に楽しく数えることなどが、成長を促すポイントになります。

よくお風呂で「いーち、にーぃ、さーん…」と数えますよね。

それだけでもとても良い練習になっています。

プリントなどであれば、

１→２→３→〇→５

「〇に入る数字は何？」のようなものが一般的ですね。

「ぼく、〇番目に座ったよ！」など、そういったことを話してくれるようになったら、

これは序数性が習得されている合図になります。

〇基数性(きすうせい)

私が支援しているお子様の中では、序数性よりも基数性が習得されていないお子様が多いです。

基数性の方が、こちら側が気付かずに埋もれてしまい易いのです。

基数性とは、量に関する概念です。

突然ですが、ミカンは何個ありますか？

はい、４個です。私たちからすると簡単ですよね。

しかし、基数性が上手く習得されていないと、「いち、に、…」というように

指で数えていくことになります。序数性で基数性を補う形ですね。

基数性が習得されていると、量を見てパッと答えることが出来ます。

他の例も挙げておきますと、分厚い辞書を用意して、「○○ページって大体どこら辺かな？」

と言って、おおよそのページを考えて当てられるといった感じです。

生活面においても、塩を大体どれくらい入れれば良いかな？など、

量について考えなければならないことって沢山ありますよね。

基数性が身についていないお子様は、こういったことが苦手な傾向があります。

学習面の影響で考えると、指を使わないと計算が出来ないということが真っ先に挙げられます。

これは、上のみかんの絵の時のように、序数性で基数性を補っている形です。

また、算数の文章題を読んで、それが増えることなのか、それとも減ることなのかなど、

そういったことを考えるのが苦手になります。

「なんでこの文章が引き算なの？」と突っ込みたくなったことってありませんか？

ついついふざけてやっているのかと思ってしまうこともありますが、

これは序数性もそうですが、何より基数性が育っていないことが原因なのです。

足し算や引き算以外に、基数性を必須とする算数の代表例が割り算の筆算です。

例えば、３６４÷５という問題があった時、まずは「３６に５っていくら入るかな？」

と考えるのが基本ですが、基数性が上手く習得されていないと難しくなってしまうわけです。

このように、１、２年生は指などを使って乗り切れても、３年生からはそれも難しくなります。

では、この概念を

どうやって育ててあげれば良いのでしょうか？

まずは、一般的な指導方法についてお話します。

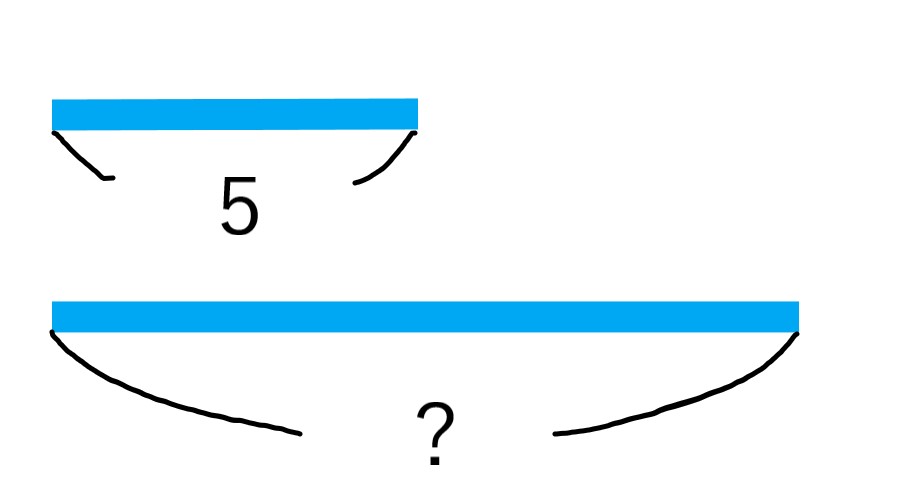
この直線、上が「５」だとすると、下はいくら？

これを考えてもらいます。

私たちは「大体２倍だから１０かな？」と考えますが、基数性が育っていないと

結構難しく感じたり、見当違いな数字になることもあります。

実際に手を動かしてもらうなら、以下のような指導方法もあります。

シールを貼っていったら、何枚貼れるかな？

１０枚貼れました。じゃあ、これは何枚貼れるかな？

この場合は上を見ると４や５と答えられると思いますが…。

このような感じで量に関する概念を育てていきます。

上のような指導ではなくても、身の周りには量について考えなければならないことが沢山あります。

料理で水の量をはかることなどもそうですし、お買い物などのお金に関するやりとりなど、

こういったことすべてが基数性に関わります。

一緒に料理をする際に何かを量ってもらったり、レジで代わりにお金を出してもらったり…。

これらを楽しく一緒にやってみることが、実は基数性を育てることに繋がるのです。

遠足のお菓子のように、予算内でお買い物をしてもらうのも良いかも知れませんね。

小学校１年生のお子様の学習課題に関して言えば、「いくつといくつ」の単元が大事です。

学校でも足し算の前に勉強はしますが、すぐに終わってしまうことが多いです。

不足しているなと感じたら、これに関わる勉強をすると良いでしょう。

プリントはインターネット上からダウンロード出来る問題が沢山ありますし、

具体物を使ったり、クイズ形式のような雰囲気でやっても良いと思います。

また、遊びに関しては、スゴロクなどが効果的でしょう。

数字が大事な要素の遊びですし、進む数によって数字の大きさも関わってきますからね。

こう考えてみると、数字に関することって、世の中に沢山あふれていますよね。

あなたも、お子様が夢中になれることや、一緒になって楽しんで取り組めることを考えてみて下さい。

〇おわりに

いかがでしょうか？

足し算や引き算など、しっかりと計算するためには、

まずは数字、数詞、具体物のマッチングが出来ること(数の三項関係)。

そして序数性と基数性の２つの概念をしっかりと育てることが大事です。

これらがきちんと確立すれば、それが土台となって算数が積み重なり易くなります。

しっかりと育ててあげて下さいね。

体験療育を実施しています。ご相談なども承っております。

お気軽に、お電話やホームページを通してお問い合わせ下さい。

では、今回はこの辺で。

こどもサポート教室クラ・ゼミ札幌東苗穂校第２

住所：札幌市東区東苗穂９条２丁目１７－３７昭輝ビル２階

電話番号：０１１－７９１－２０７５

営業時間：１０時から１９時(日曜は休業日)